42 接雨水
经典字节跳动必考算法之接雨水
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
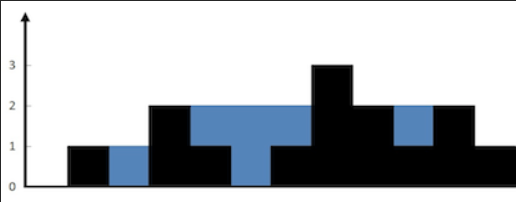
输入:height = [0,1,0,2,1,0,1,3,2,1,2,1] 输出:6 解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
输入:height = [4,2,0,3,2,5] 输出:9
n == height.length1 <= n <= 2 * 1040 <= height[i] <= 105
方法一 动态规划
// 1. 从左向右遍历,找到每个柱子左侧的最大值
// 2. 从右向左遍历,找到每个柱子右侧的最大值
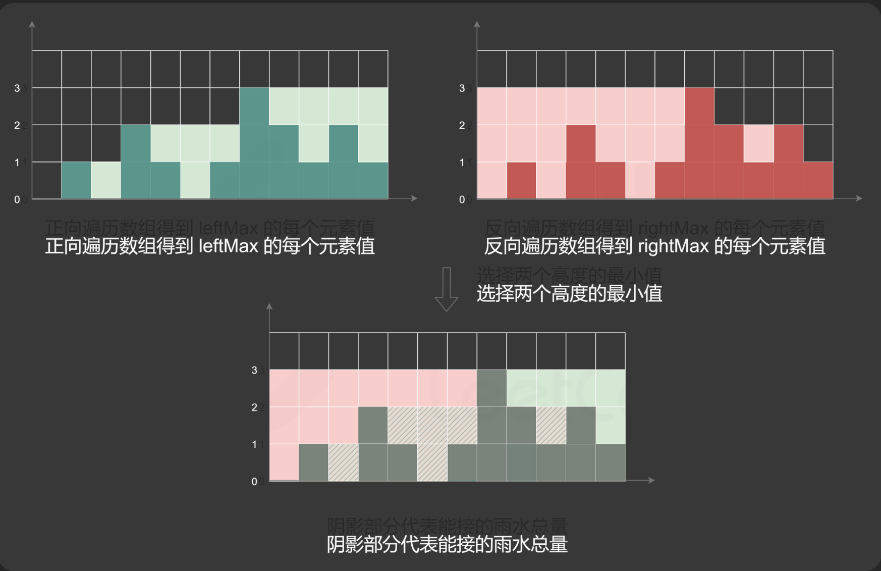
// 3. 遍历每个柱子,计算每个柱子的蓄水量
var trap = function(height) {
const n = height.length;
if (n == 0) {
return 0;
}
const leftMax = new Array(n).fill(0);
leftMax[0] = height[0];
for (let i = 1; i < n; ++i) {
leftMax[i] = Math.max(leftMax[i - 1], height[i]);
}
const rightMax = new Array(n).fill(0);
rightMax[n - 1] = height[n - 1];
for (let i = n - 2; i >= 0; --i) {
rightMax[i] = Math.max(rightMax[i + 1], height[i]);
}
let ans = 0;
for (let i = 0; i < n; ++i) {
ans += Math.min(leftMax[i], rightMax[i]) - height[i];
}
return ans;
};2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
方法二 单调栈
// 1. 遍历每个柱子,如果栈不为空且当前柱子高度大于 栈顶柱子高度 ,弹出栈顶元素
// 2. 计算当前柱子和栈顶柱子之间的蓄水量 长乘宽
// 3. 将当前柱子入栈
// 4. 遍历结束后,返回蓄水量
var trap4 = function(height) {
let ans = 0;
const stack = [];
const n = height.length;
for (let i = 0; i < n; ++i) {
while (stack.length && height[i] > height[stack[stack.length - 1)) {
const top = stack.pop();
if (!stack.length) {
break;
}
const left = stack[stack.length - 1];
const currWidth = i - left - 1;
const currHeight = Math.min(height[left], height[i]) - height[top];
ans += currWidth * currHeight;
}
stack.push(i);
}
return ans;
};2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
方法三 双指针
蓄水量 由左侧最高柱子和右侧最高柱子中,较矮的那个柱子决定
注意到下标 i 处能接的雨水量由 leftMax [i] 和 rightMax [i] 中的最小值决定。由于数组 leftMax 是从左往右计算,数组 rightMax 是从右往左计算,因此可以使用双指针和两个变量代替两个数组。
维护两个指针 left 和 right,以及两个变量 leftMax 和 rightMax,初始时 left=0,right=n−1,leftMax=0,rightMax=0。指针 left 只会向右移动,指针 right 只会向左移动,在移动指针的过程中维护两个变量 leftMax 和 rightMax 的值。
当两个指针没有相遇时,进行如下操作:
使用 height [left] 和 height [right] 的值更新 leftMax 和 rightMax 的值;
如果 height [left]<height [right],则必有 leftMax<rightMax,下标 left 处能接的雨水量等于 leftMax−height [left],将下标 left 处能接的雨水量加到能接的雨水总量,然后将 left 加 1(即向右移动一位);
如果 height [left]≥height [right],则必有 leftMax≥rightMax,下标 right 处能接的雨水量等于 rightMax−height [right],将下标 right 处能接的雨水量加到能接的雨水总量,然后将 right 减 1(即向左移动一位)。
当两个指针相遇时,即可得到能接的雨水总量。
const trap = function (height) {
let left = 0;
let right = height.length - 1;
let leftMax = 0;
let rightMax = 0;
let ans = 0;
while (left < right) {
const leftHeight = height[left];
const rightHeight = height[right];
if (leftHeight < rightHeight) {
leftMax = Math.max(leftHeight, leftMax);
ans = ans + leftMax - leftHeight;
left++;
} else {
rightMax = Math.max(rightHeight, rightMax);
ans = ans + rightMax - rightHeight;
right--;
}
}
return ans;
};2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21